QUELQUES BOULES DE PÉTANQUE ...
En caricaturant un peu, car comme chacun sait, nous dessinons en 2D, nous vivons en 3D, tandis que Maryna Viazovska pense, elle, en n-D et plus particulièrement ici en 8-D et en 24-D, soulignons qu'une des Médailles Fields 2022 (Olympe des récompenses mathématiques) vient de lui être attribuée pour une simple histoire de rangement optimal de boules de pétanque. Comme l'illustrent les deux photographies ci-dessus: Mieux vaut une qui sait que quatre qui cherchent.
Avec le bagage mathématique du collège, on peut s'amuser à examiner, en 2D, en 3D, quelques petits morceaux d'aspects de la situation.
Le problème simplifié en 2D est celui du rangement optimal d'une couche de boules de pétanque dans une cagette rectangulaire (on va parler de valise) dont les dimensions sont des multiples du diamètre des boules. On pourra prendre ce diamètre pour unité, la cagette est donc de dimension mxn, avec m et n entiers.
Quelle que soit la façon de ranger les boules, le problème se réduit au pavage d'un rectangle mxn par des disques de rayon unité. Si on ordonne les boules en m rangées de n boules, on occupe une surface mxnxpi/4 (car chaque disque est de surface pix(1/2)^2=pi/4 par la formule générale pixr^2 de l'aire d'un disque de rayon r). On a donc un taux d'occupation de la cagette (de surface mxn) égal à pi/4 par le quotient des aires, soit en arrondissant sur une décimale: 78,5%.
Si on essaie de décaler les boules d'une rangée sur l'autre pour exploiter le creux qui se crée entre deux boules qui se touchent, l'affaire se complique un peu, les dimensions de la cagette sont à revoir pour y ordonner sans perte un nombre entier de rangées contenant un nombre entier de boules, mais à y réfléchir, on voit que l'on peut raisonner d'abord sur des groupes de trois boules contiguës, dont les centres A,B et C sont les sommets d'un triangle équilatéral de côté unité. Raisonnant sur les disques, et nous limitant à ce triangle, lesdits disques le couvrent partiellement grâce à trois portions identiques chacune d'angle au centre 60°, c'est-à-dire pi/3, donc chacune d'aire égale au sixième de l'aire du disque, qui correspond à un angle au centre de 2pi. A eux trois, les disques couvrent donc une surface du triangle égale à pi/8. La surface d'un triangle équilatéral de côté a est donnée par la formule a^2xRac(3)/4 , où Rac désigne la racine carrée.Ici, le côté est 1. D'où l'aire Rac(3)/4 . Par quotient, le taux d'occupation du triangle équilatéral par les disques est finalement : (pi/8)/(Rac(3)/4) soit pi/(2xRac(3)), soit, avec arrondi: 90,7%
En ignorant les problèmes de bord, on voit que ce rangement - on fait comme si on pavait intégralement le rectangle par juxtaposition des triangles équilatéraux - est très supérieur en efficacité au premier. Mais justement, il y a des problèmes de bord et du coup, la situation est très ... variable.
Par exemple: soient à ranger 12 boules de pétanque, six paires. Gardons l'unité comme diamètre de la boule de base.
Dans le rangement sans décalage, quelles que soient les dimensions de la valise (1x12; 2x6; 3x4), le taux en 2D est pi/4. Dans le rangement avec décalage, la forme même de la valise nous contraint. Si elle est toujours rectangulaire (on raisonne en 2D, la valise est toujours ''d'épaisseur'' unité, il n'y a qu'une couche de boules), on va examiner séparément les options 2x6 et 3x4.
Cas 2x6 : le décalage de la seconde rangée nécessite une longueur de 6,5. En largeur, l'utilisation des creux conduit à un gain. Celle-ci est maintenant définie par la hauteur du triangle équilatéral des trois centres d'un triplet de boules (Rac(3)/2) auquel s'ajoutent deux rayons (2x(1/2) soit au total : 1+Rac(3)/2. Aire de la valise : 6,5x(1+Rac(3)/2) pour 12 boules (en 2D: disques) d'aire totale 3xpi. Le taux 2D est devenu (quotient, puis arrondi) : 77,7%
Cas 3x4 et décalages successifs alternés vers la droite, vers la gauche, d'une rangée sur l'autre:
- pour 3 rangées de 4, il nous faut une longueur de 4,5. La largeur utilise cette fois deux rayons plus deux hauteurs de triangle équilatéral, soit : 1 + Rac(3). La valise a pour surface : 4,5x(1+Rac(3)) et cette fois, le taux d'occupation 2D est : 76,6%
- gagnerait-on avec 4 rangées de 3? La valise est de dimension 3,5x(1+3xRac(3)/2), pour un taux 2D d'occupation : 74,8%
Mais on peut imaginer une valise dont la section 2D définie par la couche des boules soit un parallélogramme, par décalage toujours dans le même sens. Reprenons rapidement les trois cas ci-dessus. Les disques décalés se rangent alors dans des parallélogrammes d'angle aigu 60° et de mêmes largeurs respectives que dans les décalages alternés. Quelle est la longueur de ces parallélogrammes? Aux deux extrémités de la ligne des centres de la première rangée de disques, le dernier rayon horizontal de valeur 1/2 est remplacé par l'hypoténuse d'un triangle rectangle de longueur 1/Rac(3) (cf. schéma ci-dessous).
Cas 2x6 : longueur 5+2/Rac(3) d'où une surface égale à (1+Rac(3)/2)(5+2/Rac(3)) et finalement un taux d'occupation 2D de 82,1%
Cas 3x4 : - rangées de 4; longueur : 3+2/Rac(3), largeur 1+Rac(3); surface: (1+Rac(3))(3+2/Rac(3)) et taux d'occupation 2D de 83%
- rangées de 3; longueur : 2+2/Rac(3), largeur 1+3Rac(3)/2; surface: (1+3Rac(3)/2)(2+2/Rac(3)) et taux d'occupation 2D de 83%
Les deux derniers taux sont prévisiblement à l'identique car les valises sont les mêmes : (1+Rac(3))(3+2/Rac(3)) = 5+11Rac(3)/3 = (1+3Rac(3)/2)(2+2/Rac(3))
REMARQUE : OCCUPATION 3D DE LA VALISE DE RANGEMENT.
L'examen du taux d'occupation 3D de la valise est immédiat. L'épaisseur de la valise sera le diamètre de la couche de boule, et donc son expression (diamètre unité) est la même que celle qui donne la surface. Pour le volume des boules, d'expression générale (4/3)xpixr^3, soit ici (4/3)xpi/8, soit pour 12 boules , 2xpi, il remplace l'expression 3xpi des calculs en 2D. Les différents taux 2D deviennent les taux 3D par simple produit par 2/3.
ET SUR PLUSIEURS COUCHES ?
Peut-être des bouts, une autre fois ...



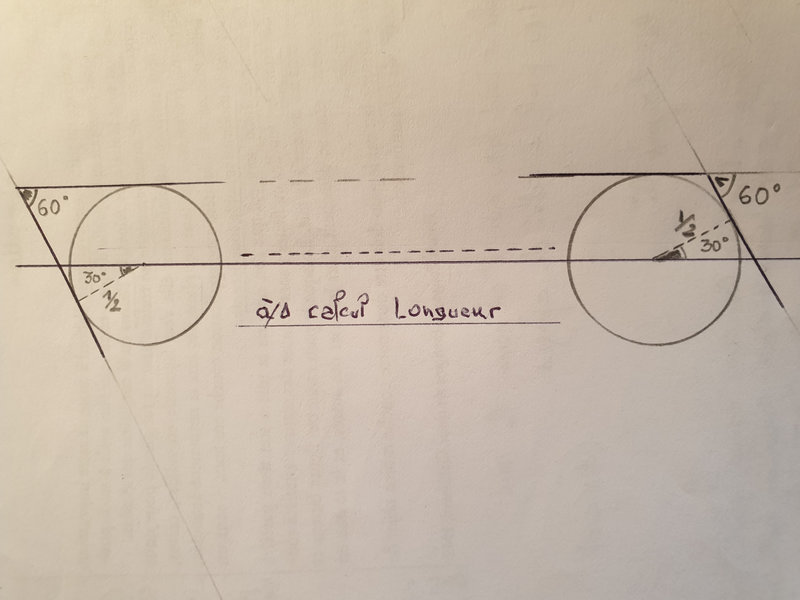




/image%2F0404595%2F20240312%2Fob_e012fa_niveau.png)
/https%3A%2F%2Fstorage.canalblog.com%2F85%2F76%2F87790%2F134452212_o.jpg)
/https%3A%2F%2Fstorage.canalblog.com%2F88%2F32%2F87790%2F134335726_o.png)
/https%3A%2F%2Fstorage.canalblog.com%2F71%2F92%2F87790%2F134316646_o.jpg)